The Cache Formula

The formula

$$\text{Set}(x)=\text{Set}(y)⟺\lfloor \frac{x}{B}\rfloor {\equiv }_S\lfloor \frac{y}{B}\rfloor$$ where $$B=\text{Blocksize}$$ $$S=\frac{\text{Cache Size}}{\text{Associativity}\cdot \text{Blocksize}}$$

Motivation

Learning about how caches work can be a very disorienting process to say the least. Worse even, learning theory may not exactly be correlated with being able to actually determine if a cache access is a hit or a miss, as one can be caught up in the hardware. Here I present a formula which abstracts most of this thinking away in favour of a very mechanical process.

Cache Basics

I will not explain the entire theory behind caches, but I find it useful to find understand where the formula comes from. Given a cache structure as follows: A cache consists of $S$ sets, of $A$ blocks (also known as the associativity) which consist of $B$ bytes (also known as the block size). If we multiply all these quantities we get $S\cdot A\cdot B=\text{Cache size}$.

Remark: It is almost always the case that all these quantities are a power of two for hardware related reasons, as such it is often ideal to write them as powers of two

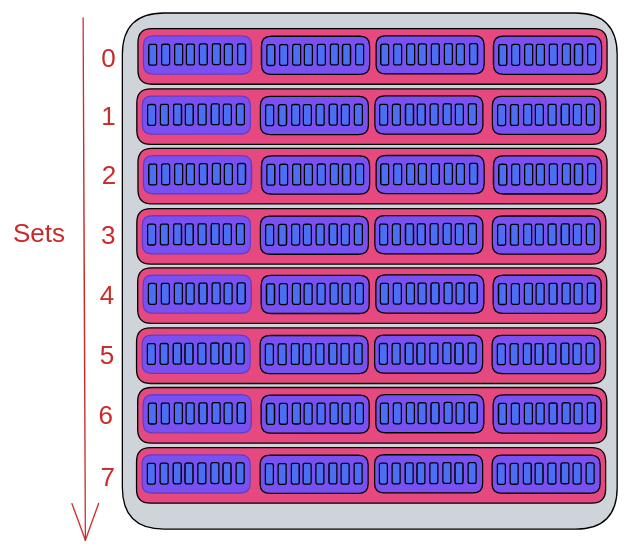
In this example we have $2^3=8$ sets in red, each set consists of $2^2=4$ blocks in purple and each block consists of $2^3=8$ bytes in blue.

Now how do we address bytes in this cache? Notice first of all that caches are designed as for cache blocks in the same cache set are meant to be shuffled around (according to eviction principles like FIFO or LRU), so we cannot address which block inside of a set something goes into. But we can address which set and what position inside of a block.

Namely we do this in binary: Assume we want the $s$-th set, the $b$-th byte in that block. Convert the numbers $s$, $b$ in binary and write them resulting binary numbers in that order.

For example $(s,b)=(1,3)$: $001$, $011$ $\Rightarrow$ we get the cache address $001011$

Notice that this is completely reversible, for example we can find that

$111000\Rightarrow 111,000\Rightarrow (7,0)$

Now we are missing the final piece of the puzzle: Given an address of a cache access how do we find its cache address? It’s easy: it’s the last few bits.

In specific notice that cache addresses always have length $L={\log }_2(S)+{\log }_2(B)$ and such we just take the last $L$ bits of an address. For example given the 32-bit address $$122478789=0111010011001110000011000101$$ In our example we take the last ${\log }_2(L)={\log }_2(S)+{\log }_2(B)=3+3=6$ bits to find that it has cache address $000101$ and therefore goes into cache set $0$ and the $5$-th position in a block.

Deriving the formula

Let $\text{Set}$ be a function which takes a given address $x$ (in decimal) and assigns it to a given cache set $s$.

In words, $\text{Set}$ writes down the decimal number in binary, then takes the last ${\log }_2(L)$ bits and then takes the first $S$ bits of that. Now notice that we can do all this by floored division and modulo operators:

$$\text{Set}(x)=\lfloor \frac{x\mathrm{\%}L}{S}\rfloor$$ Alternatively we can also that $\text{Set}(x)$ removes the last $B$ bits and then takes the last $S$ bits of what is left: $$\text{Set}(x)=\lfloor \frac{x}{B}\rfloor \mathrm{\%}S$$ Therefore, two addresses map to the same set if $$\text{Set}(x)=\text{Set}(y)⟺\lfloor \frac{x}{B}\rfloor \mathrm{\%}S=\lfloor \frac{y}{B}\rfloor \mathrm{\%}S⟺\lfloor \frac{x}{B}\rfloor {\equiv }_S\lfloor \frac{y}{B}\rfloor$$

What about Associativity?

One may notice that Associativity does not actually occur in this formula. This may lead to the conclusion that associativity never has to be considered when asking if two addresses map to the same set. This is correct with a big asterik.

Namely, we almost never have the numbers $B$ and $S$ as such. It is much more common to have Cache Size, Associativity $A$ and only Block size $B$. $S$ is therefore determined by $$S=\frac{\text{Cache Size}}{A\cdot B}$$ And therefore the above formula is more easily written by: $$\text{Set}(x)=\text{Set}(y)⟺\lfloor \frac{x}{B}\rfloor \mathrm{\%}S=\lfloor \frac{y}{B}\rfloor \mathrm{\%}S⟺\lfloor \frac{x}{B}\rfloor \mathrm{\%}\frac{\text{Cache Size}}{A\cdot B}=\lfloor \frac{y}{B}\rfloor \mathrm{\%}\frac{\text{Cache Size}}{A\cdot B}$$ $$⟺\lfloor \frac{x}{B}\rfloor \mathrm{\%}\frac{\text{Cache Size}}{A\cdot B}=\lfloor \frac{y}{B}\rfloor \mathrm{\%}\frac{\text{Cache Size}}{A\cdot B}$$ One may notice now that increasing $A$ directly increases the chance that $x$ and $y$ map to the same set. To actually use the formula, I would recommend just calculating $S$ and then using the formula dependent on $S$.